平面曲线的切线和法线
空间曲线的切线与法平面
参数方程
一般方程
例题
参数方程
一般方程
曲线的切线和法平面
分类： 数学趣识
统计学假设检验中p值的含义具体是什么？
摘录自 https://www.zhihu.com/question/23149768[全文]
1.假设检验
- 你提出假设：说你的硬币是公平的
- 我提出要检验你的假设：扔十次，看实验的结果是不是和你的假设相符
反复扔硬币应该符合二项分布（这就不解释了），也就是：
其中，n 代表扔硬币的次数， μ 代表“花”朝上的概率。
在我们认为硬币是公平的前提下，扔10次硬币应该符合以下分布：
下图表示的就是，假如硬币是公平的情况下的分布图：
我扔了十次之后得到的结果是，有八次正面：
2.P值
罗纳德·艾尔默·费希尔爵士（1890－1962）
把八次正面的概率，与更极端的九次正面、十次正面的概率加起来：
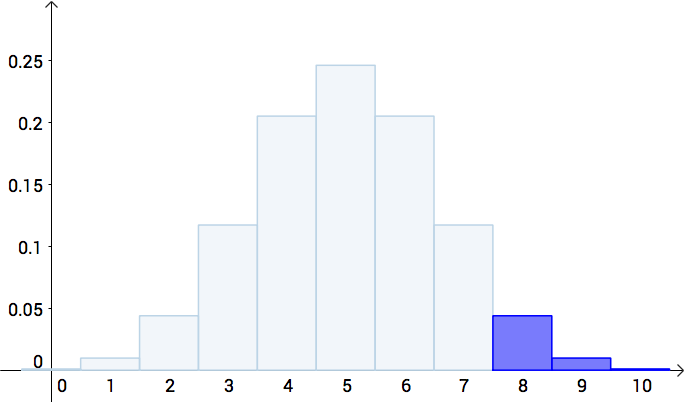
得到的就是（单侧P值）
其实，出现两次正面、一次正面、零次正面的概率也是很极端的：
所以（双侧P值）：
- 取单侧还是双侧，取决于你的应用
- 什么叫做更极端的点，也取决于你的应用
3.显著水平
总共扔10次硬币，那么是出现7次正面之后，可以认为“硬币是不公平的”，还是9次正面之后我才能确认“硬币是不公平的”，这是一个较为主观的标准。
我们一般认为
0.05这个标准就是显著水平，当然选择多少作为显著水平也是主观的。
比如，上面的扔硬币的例子，如果取单侧P值，那么根据我们的计算，如果扔10次出现9次正面：
4 .与置信区间的关系
置信区间，目的是根据样本构造一个区间，然后希望这个区间可以把真值包含进去，但是并不知道这个真值是多少？具体可以参考 如何理解 95% 置信区间？
而假设检验，则是假设真值是多少，然后检验这个假设是否可能为真。
之所以觉得它们有关系，大概是因为它们都提到了0.05
它们之间的关系也简单，如果我们提出来的假设 μ0在样本 x 的置信区间内，就可以通过测试：
反之，就不能通过：
格林公式
例题
计算面积
计算积分
理解
作者：撒欢猪宝
链接：https://www.zhihu.com/question/22674439/answer/165988374
来源：知乎
看了一下各位答主的回答，都很专业和清楚，我尝试用我的方式来解释格林公式，给出一个不一样的理解角度。
另外，有一个答主说格林公式用旋度来解释，是我最赞同的，不过目前可能大家还没有理解旋度的本质，所以我先不引入旋度了。
格林公式有点难以理解，因为它确实有些反直觉，“我们为什么能够用内部的情况来描述外围的情况？”看到公式后很多人会产生这个疑问，公式是一步登天的，是对最终结论的简洁描述，所以在我们得出结论之前，不妨先解决一个个的小问题，给自己搭一个个小台阶，最终完美的理解问题。数学如此，科学上任何事物皆是如此。
所以在正式讨论格林公式之前，我们先用语言来描述这个奇怪的公式：
有一条光滑连续的封闭曲线L，这个L是封闭的所以肯定会围成一个区域叫做D，同时这块区域上存在着一个力场F，根据坐标的不同力场中每一点都会收到力的作用，如下图所示：
好，让我们来提出一个问题，作为我们的目标。请求出沿着曲线L的力们做的总功。
这是一个很实际的问题，现实生活的运动中不可能永远是高中物理题中的直线运动或者完美的圆周运动，所以还没有微积分的时候，这种问题都是难以解决的，而现在我们有了微积分这个武器，所以聪明的我们立刻想到了一个解决方案：
把这个封闭曲线L分解成无数个小段，每个小段近似直线，在这条直线上的力F可以看成不变，求出每一段直线上的做功，然后在求一个和，问题迎刃而解！我们用一张图来描述这个解决方案：
受过高等教育的我们发现，即使简化到这一步，我们依然难以用一个数学表达式来描述这个总功，因为F力的方向和小直线段的方向不一样且夹角也未知，于是我们进一步的把力F分解成沿x方向和沿y方向，同时也将线段这么分解，到这里我们可以写出总功的公式了：
问题看似已经解决，但是我们出现了一个问题：该如何求这个积分呢？
你可能会想到用y=f(x)来将这个积分化简为一元函数积分
但是很遗憾这不可行，因为这是一个封闭曲线，他违反了函数的垂直线校验（不知道的自行百度 函数的垂直线校验），这意味着你压根不可能写出一个y=f(x)的式子，遇到这个大麻烦了，该如何解决呢？乔治·格林同志将运用他天才的大脑给出我们一个解决方案，而我将猜测性的复盘他的思维过程。
休息一下，累死我了。
格林同志认为，复杂的事情可以先从简单的模型入手：
他假设这么一个矩形，求矩形上力们沿着矩形做功，然后，他跨出了重要的一步，他把两个矩形拼到了一起：
你可能还没有意识到这一步有多么重要，那我就要提示你一下，看到这两个矩形重合的那条边了吗，注意，这条边上的每个点的力都完全相同，唯一不同的是做功的方向正好相反！这意味着这一段的做功抵消掉了，于是这两个矩形的总功可以简化成这样：
你可以继续叠加成三个矩形、四个矩形，你会发现当多个旋转方向相同的矩形叠加在一起时，他们内部的做功全部抵消掉了！只剩下最外围那个轮廓做的功！
也许格林同志意识到这一点的时候笑出了声，你是不是还没有意识到他为什么笑了，这只是一个矩形的简单模型啊，我们要求的问题是复杂的不规则光滑封闭曲线啊！但是你看看格林用他的微积分知识画了这样一张图：
与我们用微积分把曲线分解成无数个小直线段不同，格林用微积分把这个区域分解成了无数个小矩形！还记得我们之前那个简单模型吗？这一大堆拼凑在一起的矩形的最外边缘的做功就是所有小矩形做功的总和！
到目前为止，我们的小台阶已经搭起来了，现在离我们最终解决问题已经不远了，我们迫切的想要知道，对于分解出来的小矩形，做功应该如何求？
又累了，再歇会。
我们取任意一个微小的微分矩形：
这就是一个任取的微分矩形，我在四个顶点处将该点所受的水平方向力P(x,y)和垂直方向力Q(x,y)标注出来了，运动方向是逆时针，由于是微分矩形，我们可以假设在沿着某一边运动时，力的大小是不变的，于是我们可以求出这个微分矩形上力做的功为：
对于这个式子，不仅是我们，连格林也一筹莫展，不过我们之前说过，这个矩形是微分矩形，当力沿着直线移动时并不改变大小，于是这个式子我们可以进行如下改造：
这张图有一处笔误，我等会纠正。
这就是这一个微分矩形做的功，那么所有的微分矩形做的功呢？积分就可以啦。再根据我们前面搭的台阶：矩形们的总功之和就是外围轮廓上做的功，那么不就得吃结论了吗！
乔治·格林写下了最终结论：
以上。
交换积分次序
多元复合函数的求导
多元复合函数
f(u(x,y),v(x,y))
关于x,y存在偏导数的充分条件
u,v关于(x,y)的偏导数连续，以及f关于(u,v)的偏导数连续
关于x的偏导数
f[x]=f[u]*u[x]+f[v]*v[x]
多元复合函数的常见形式
例题
摘自https://wenku.baidu.com/view/08371d1b9b89680202d825af.html
第一类曲线积分
第一类曲线积分
对弧长的∫[L] f(x,y) ds
计算方式
三种情况计算例题
1、x= x(t) , y=y(t) , t∈[a,b]
∫[a,b] f{x(t) , y(t)} * {x'(t)^2+y'(t)^2}^0.5 dt
2、x=x，y=y(x) , x ∈[a,b]
∫[a,b] f{x , y(x)} * {1+y'(x)^2}^0.5 dx
3、x=rcosθ， y=rsinθ ，r=r(θ)，θ∈[a,b]
∫[a,b] f{r(θ)cosθ , r(θ)sinθ } * { r(θ) ^2 +r'(θ) ^2}^0.5 dθ
利用对称性计算
方向导数
可微二元函数的方向导数
二元函数方向导数定义计算
有趣的雪花图形
数学中的雪花图形由一个简单的正三角形开始，每一次变化的图形都是前一个图形的每条边正中央长出一个周长等于该边的正三角形。
由于雪花图形定义是递推的。因此利用递推公式可证明图形雪花图形的周长是发散的，但是面积却是收敛的。证明如下。
雪花图形的边长公式推导
雪花图形的面积公式推导
因此数学中有名的雪花图形是科赫曲线。
PS:上述推演存在肉眼可见计算错误😓~，系数差异 ，不影响结论
ellen's blog 